



菲利普·格拉斯
生平格拉斯1937年生于美国马里兰州巴尔的摩,祖上是立陶宛犹太人,因为父亲开了一家音像店而从小对从贝多芬到肖斯塔科维奇的各个时期的古典音乐都有所涉猎,后来就读于朱利亚音乐学院,又赴巴黎受教于娜迪亚&m
生平
格拉斯1937年生于美国马里兰州巴尔的摩,祖上是立陶宛犹太人,因为父亲开了一家音像店而从小对从贝多芬到肖斯塔科维奇的各个时期的古典音乐都有所涉猎,后来就读于朱利亚音乐学院,又赴巴黎受教于娜迪亚·布朗热。后来与印度音乐家拉维·香卡合作后对非西方音乐发生了浓厚兴趣,并独立发展出了自己的简约主义风格。他的音乐创作往往涉及世界各地的不同文化。在谈到自己的信仰时,格拉斯曾说自己是“犹太-道教-印度-托尔特克-佛教徒”。
音乐风格及创作
格拉斯的简约主义风格深受东方文化和流行音乐的影响,他的作品往往在一个牢固的自然音框架之中以五六个音符作为基础,没有和声变化而节奏极度稳定。 他的音乐是有调性的,有的甚至带有浪漫主义式的旋律感,例如《第一小提琴协奏曲》。
格拉斯还是一位重要的电影配乐作曲家,近期的著名电影音乐包括《楚门的世界》以及《时时刻刻》。
参见
古典音乐作曲家列表
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。
——— 没有了 ———
编辑:阿族小谱

文章价值打分
- 有价值
- 一般般
- 没价值
当前文章打 0 分,共有 0 人打分
文章观点支持

0

0
文章很值,打赏犒劳一下作者~

发表评论
写好了,提交
{{item.label}}
{{commentTotal}}条评论
{{item.userName}}
发布时间:{{item.time}}
{{item.content}}
回复
举报


打赏作者
“感谢您的打赏,我会更努力的创作”
— 请选择您要打赏的金额 —
{{item.label}}


{{item.label}}

打赏成功!
“感谢您的打赏,我会更努力的创作”
返回
打赏
私信
24小时热门
推荐阅读
· 格拉斯

地理位置与概况格拉斯坐落在法国地中海沿岸海边,属于法国东南部普罗旺斯-阿尔卑斯-蓝色海岸大区滨海阿尔卑斯省。南边12公里处是嘎纳,东北边距离29公里处是滨海阿尔卑斯省的省会尼斯,距离法国首都巴黎677公里。格拉斯行政面积为4444公顷(44.44平方公里)。大部分面积由森林覆盖。比较其他市镇,格拉斯不仅面积广阔,地势也陡峭,海拔高度变化很大。从临海到内陆,海拔逐渐增高,在平均300余米的纬度差别下,海拔可以从不到100米,增加到1000米。经济香水格拉斯是法国香水业的中心,被誉为世界香水之都。自从18世纪末以来,格拉斯的香水制造业一直相当繁荣。该镇号称“世界香水之都”(lacapitalemondialedesparfums),生产法国三分之二的天然aromas,用于制造香水和食品调味料。每年香水业为格拉斯创造超过6亿欧元的财富。格拉斯特殊的小气候非常适合花卉种植。这里较为温暖,而且距离海...
· 格拉斯区
辖区格拉斯区辖有19个县,共有62个市镇。
· 拉格拉斯里
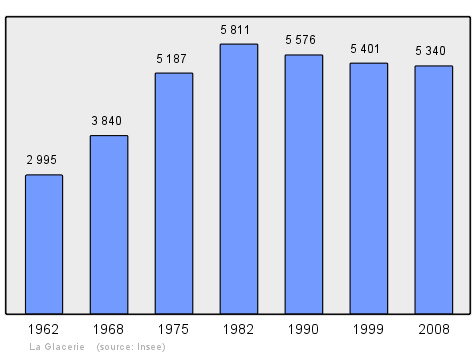
人口拉格拉斯里人口变化图示参见芒什省市镇列表
· 格拉斯哥

历史市政局徽章格拉斯哥的城市名由来,源自布利屯语中的“glaschu”,意指“绿色的空地”。格拉斯哥地区早在公元前已有部落聚居。后来,古罗马人在此地区设立了前哨站,建筑了安多宁长城来分隔当时南部古罗马管辖的不列颠尼亚和北部的加勒多尼亚。基督教传教士圣穆格(SaintMungo)于6世纪在此建立了格拉斯哥大教堂,为格拉斯哥日后发展立了基础。到了12世纪,格拉斯哥已有了相等于今日所谓城市的地位。1451年,格拉斯哥建立格拉斯哥大学。在16世纪初,格拉斯哥已是重要的宗教与学术城市。格拉斯哥独特的地理位置也使其成为对美洲贸易的重要中心,商人从美洲大量输入美国烟草和加勒比海地区的白糖,然后再转售至不列颠群岛和欧洲大陆的其他地方。富庶的烟草商用财富大兴土木,对格拉斯哥城市建设起到了关键作用,市中心多条街道名取自当年的烟草商人名。1770年代克莱德河的加深使到较大的船只也可航行到河的更上游。这对19世纪...
· 格拉斯曼流形
引言通过给定子空间一个拓扑结构可以谈论子空间的一个连续选取或子空间集合的一个开集或闭集;通过给它们一个微分流形结构可以考虑子空间的光滑选取。一个自然的例子来自嵌入在欧几里得空间中光滑流形的切丛。假设我们有一个r维流形M嵌入在Rn{\displaystyle\mathbb{R}^{n}}中。在M中的每一点x,M的切丛可以视为Rn{\displaystyle\mathbb{R}^{n}}的切空间(也是Rn{\displaystyle\mathbb{R}^{n}})的一个子空间。将x分配为它切空间定义了一个M到Grr(n)的映射。(为此我们需要平移M在x处的切空间到原点,从而定义了一个r-维向量子空间。这种想法非常类似于三维空间中曲面的高斯映射)。这种想法广泛地说可以推广到一个流形M所有向量丛,这样每个向量丛产生一个从M到一个合适的一般化格拉斯曼流形的连续映射——但是为此我们须证明不同的嵌入定理...
关于我们

关注族谱网 微信公众号,每日及时查看相关推荐,订阅互动等。
APP下载

下载族谱APP 微信公众号,每日及时查看

扫一扫添加客服微信

















