都在等待“黎曼猜想”证明

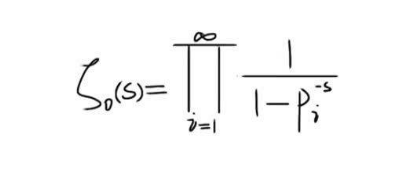
　　却不知道它后面隐藏的危险

　　一、大神黎曼

　　过直线外一点，可作其几条平行线?

　　欧氏几何说，只能作一条;

　　罗氏几何说，至少可以作两条(包括一组和无数)。

　　黎曼慢悠悠地反问：谁知道平行线相交还是不相交呢?

　　“平行线公理”的世纪之争，最终终结于黎曼。

　　黎曼提出：过直线外一点，一条平行线也作不出来。(这是人话吗?)

　　可基于黎曼几何得出的“无平行线”结论，最终成了广义相对论的数学帮手。

　　广义相对论最初源于爱因斯坦意识到引力并不是一种力，而是时空几何弯曲的体现。

　　物理直觉超于常人的爱因斯坦一直找不到数学工具来表达他的想法，如果没有数学支撑，直接说引力是时空弯曲效应，肯定会被吐槽成“物理是体育老师教的”。

　　所以，直到他从数学界朋友了解到黎曼的“非欧几何”，才让广义相对论提早问世。当爱因斯坦得意地跟全世界说：如果没有我，50年内也不会出现广义相对论。

　　这时候，能和爱因斯坦站在一起吹牛的，也只有数学大神黎曼了。

　　二、黎曼猜想与裸奔的互联网

　　“几何”一直是黎曼的主业，这又是一座深不可测的数学殿堂。

　　但今天聊的不是他的主业，而是他在1859年“闲暇之余”随手丢下的一个猜想。

　　这个猜想说的是：存在一个对素数分布规律有着决定性影响的黎曼ζ函数①非平凡零点②。

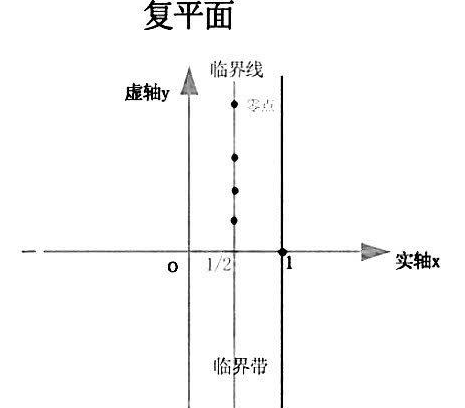
　　关于这些点，容易证明它们都分布在一个带状区域上，黎曼认为它们的分布要比这个容易证明的结果齐整得多，他猜测它们全都位于该带状区域正中央的一条直线上。而这条被猜测为包含黎曼ζ函数所有非平凡零点的直线则被称为临界线。就这样，黎曼猜想正式被提出。

　　讲人话，我们来看黎曼猜想到底长什么样纸!

　　首先定义一个函数叫黎曼函数：

　　ζ(s)= 1 + 1 / 2^s+ 1 / 3^s+ 1 / 4^s+……

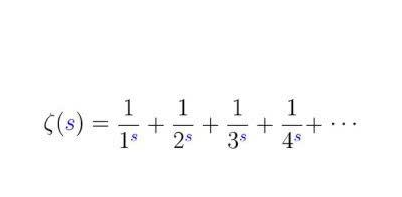
　　黎曼猜想指的是：黎曼函数所有非平凡零点的实部都是1/2。更通俗的数学表达式如下：

　　ζ(s)= 1 + 1 / 2^s+ 1 / 3^s+ 1 / 4^s+……=0的所有非平凡解都在直线x=1/2上。

　　怎么样!看懂了吧，如果还有疑问……那我也没辄了，我的智商有限。

　　黎曼自己肯定没有想到，他所提出的这个猜想，足足折腾了数学家们159年。

　　如果黎曼知道直到2018年我们还在纠结，一定会花点时间把证明写出来的。

　　这件事情还得怪他的老师高斯，高斯的座右铭是“宁肯少些，但要成熟”的低调作风，这一点影响到黎曼，让他成为一个惜字如金的大神。

　　他一生仅发表过10篇论文，但每篇论文都横跨各领域，是多领域的先锋开拓者，虽然不到40岁就去世，但仍然显示出不可一世的才华。

　　1859年黎曼抛出的这个不朽谜题，就是想解决素数之秘。

　　一旦素数之秘被解开，那么现在几乎所有互联网的加密方式将不再安全，变成一个裸奔的世界，因为我们主要的非对称加密包括RSA密钥加密等等，都是基于大数的分解。

　　不仅仅是互联网，只要证明方法被公布，无需量子计算机，根据其原理甚至能破解现代银行的安全密码体系，看你还开心不开心!

　　三、非对称加密算法和素数的关系

　　那些担心自己的钱包和黎曼猜想的朋友们，我们再复习一下小学数学：

　　小于20的素数有多少个?答案是有8个：2、3、5、7、11、13、17和19。小于1000的素数有多少个?小于100万呢?小于10亿的呢?

　　观察素数表，你会发现素数数目是下降的，它们越来越稀疏。1和100之间有25个素数，401和500之间有17个，而901和1000之间只有14个。如果把素数列到100万，最后一个百数段(就是从999901到1000000)中只有8个素数。如果列到10 000亿，最后一个百数段中将只有4个素数。它们是，999 999 999 937，999 999 999 959 ，999 999 999 961，999 999 999 989。

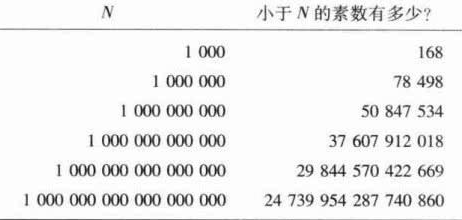
　　越到后面，素数的寻找越发艰难。

　　这样，聪明的数学家们将素数应用在密码学上，因为人类还没有发现素数的规律，以它作密钥进行加密的话，破解者必须要进行大量运算，即使用最快的电子计算机，也会因求素数的过程时间太长而失去了破解的意义。

　　现在普遍使用于各大银行的是RSA公钥加密算法 ，基于一个十分简单的素数事实：将两个大质数相乘十分容易，但是想要对其乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥。

　　黎曼猜想得到完全证明，很有可能派生出攻击RSA公钥加密算法的规律。

　　一旦黎曼猜想得证，那么基于大素数分解的非对称加密算法可能就走到了尽头，私钥加密、签名也就失去了意义。

　　当我们在为数学家开心的时候，也得小心那些寻找漏洞的黑客。

　　四、黎曼ζ函数证明和量子幽灵有关吗?

　　黎曼猜想的证明有那么难吗?在这里我不列出这些证明细节，只看看一路坎坷的证明历程：

　　1、1896年，法国的哈达玛抵达猜想的三八临界线边缘——证明了黎曼ζ函数的非平凡零点只分布在带状区域的内部，并顺手干掉了刁难人类一百年的素数定理。

　　2、1914年，丹麦的玻尔与德国的兰道触到了冰山一角，窥得了黎曼ζ函数的非平凡零点倾向于“紧密团结”在临界线的周围。

　　3、英国的哈代副武装模式开启，直接将“红旗”插上了临界线——证明了黎曼ζ函数有无穷多个非平凡零点位于临界线上。

　　4、1989年美国的康瑞又推翻了列文森的推论，重新开启了估算的新篇章，又证明了至少有40%的零点位于临界线上。

　　……

　　然而谁也没能真正搞定黎曼猜想，数学上“无穷大”这只恶魔让再多数值证据都微不足道。

　　没想到，有幸之年，我竟能亲身见证黎曼猜想被证明，若为真，实深感荣焉。

　　就在最近，2018年9月20日，菲尔兹和阿贝尔奖双料得主迈克尔o阿蒂亚爵士宣称自己证明了黎曼猜想，要在9月24日海德堡获奖者论坛上向全世界公布证明。

　　一听这消息，躲在深山老林的科学家们全炸了。

　　黎曼猜想这次真的会被解决吗?作为数学奖最高得主，阿蒂亚爵士的确是这个时代顶尖数学家之一，但他都89岁了，会不会只是出来玩票……

　　另外，阿蒂亚爵士还有点“嚣张”地声称证明并不复杂(毕竟这猜想还是苦了人类159年)，是基于之前冯诺依曼、希策布鲁赫、狄拉克的工作。

　　冯o诺依曼，计算机之父，以研究算子理论、量子理论闻名遐迩。

　　希策布鲁赫，恕我孤陋寡闻，不知道他是干嘛的。

　　狄拉克，预言了反物质的那个家伙，量子力学顶梁柱人物之一。

　　一看，除去那个我不太熟悉的，此次证明恐与量子力学有着千丝万缕的关系。

　　自20世纪以来，已有部分科学家注意到素数与量子物理之间存在联系。

　　黎曼猜想中的素数行为，酷似量子力学中的“测不准原理”，虽然你可能不知道单个分子确切位置，但是你可以确定这个房间大致的分子分布，素数这难以捉摸的行为特别像量子幽灵掌握的微观世界。

　　阿蒂亚若是借助量子力学这一工具来解决黎曼猜想也不是不可能。毕竟，数学中很多重大问题，都是建立在与其他数学分支跨界联系的基础上才被解决，比如费马大定理。

　　而由量子理论所衍生而出的量子计算机，也早已被数学家证明能快速对大数进行质因数分解，基于“平行世界”的运算可轻而易举破解素数并颠覆密码系统。

　　量子力学与素数的恋情，也许将在这一次揭开情人面纱。

　　五、猜想将动摇数学大厦吗?

　　各大行长躲在银行保险柜前瑟瑟发抖，不少黑客则潜伏敲着键盘蓄势待发。

　　一旦证明方法得证无误，密码夹持着的无尽秘密有多少会不复存在。

　　然而，黎曼猜想带来的危险不仅仅影响银行，更不仅仅是互联网，甚至可能动摇到一些数学根基。

　　数学文献中已有超过一千条数学命题以黎曼猜想的成立为前提。如果黎曼猜想被证明，所有那些数学命题就全都可以荣升为定理;反之，如果黎曼猜想被否证，则那些数学命题中起码有一部分将成为陪葬品。

　　那些建立在黎曼猜想上的推论，可谓是一座根基不稳、摇摇欲坠、令人惶恐不安的大厦。

　　一个数学猜想与为数如此众多的数学命题有着密切关联，这是世上极为罕有的，也许正是因为这样的关系，黎曼猜想的名气和光环变得更加显著，也越发让人着迷。

　　因而，此次黎曼猜想是否成功证明，将牵一发而动全身，直接影响以黎曼猜想作为前提的数学体系。

　　六、危险的数学和逝去的“爱神”

　　伯恩哈德o黎曼于1866年7月20日去世，离开这个世界时还不到40岁。

　　天妒英才，这位与欧拉、高斯、伽罗瓦一样在数学上具有顶尖天赋的人物，可能因为其才华带来巨大危险，很快就被上帝唤回去打麻将了。

　　他并没有意识到自己对这个世界的影响会如此深远，临走之前非常安宁，没有挣扎也没有临终痉挛，仿佛饶有兴趣地观看灵魂与肉体的分离。

　　《素数之恋》一书谈到：他妻子给他拿来面包和酒，他要她把他的问候带给家里人，并对她说：“亲亲我们的孩子”。她为他诵读了主祷文，他的眼睛虔诚地向上仰望，几次喘息以后，他纯洁而高尚的心脏停止了跳动。

　　他长眠在塞拉斯加教区比甘佐罗教堂的院子里，墓碑上的碑文是：

　　这里安息着

　　格奥尔格o弗里德里克o伯恩哈德o黎曼

　　哥延根大学教授

　　生于1826年9月17日，布雷斯伦茨

　　卒于1866年7月20日，塞拉斯加

　　万事都互相效力

　　叫爱神的人得益处

　　注释：

　　①ζ函数：(ζ-function)用来刻画系统周期点性态的函数。

　　②零点：设是定义在数域k上的函数，我们把方程f=0在数域k中的解称作f(在k中)的零点，所有零点构成的集合称作零点集。