基础教案

　　广义相对性原理和等效原理狭义相对论认为，在不同的惯性参考系中一切物理规律都是相同的.爱因斯坦在此基础上又向前迈进了一大步，认为在任何参考系中(包括非惯性系)物理规律都是相同的，这就是广义相对性原理.

　　下面介绍广义相对论的另一个基本原理-等效原理.

　　等效原理

　　假设宇宙飞船是全封闭的，宇航员和外界没有任何联系，那么他就没有任何办法来判断，使物体以某一加速度下落的力到底是引力还是惯性力.实际上，不仅是自由落体的实验，飞船内部的任何物理过程都不能告诉我们，飞船到底是在加速运动，还是停泊在一个行星的表面.这里谈到的情景和本章第一节所述伽利略大船中的情景十分相似.这个事实使我们想到：一个均匀的引力场与一个做匀加速运动的参考系等价.爱因斯坦把它作为广义相对论的第二个基本原理，这就是著名的等效原理.

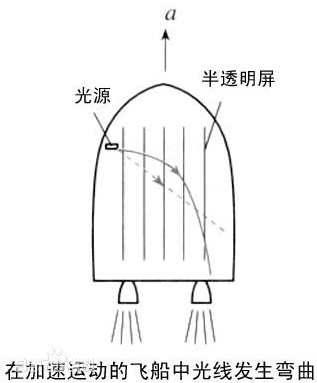
　　从这两个基本原理出发可以直接得出一些意想不到的结论.假设在引力可以忽略的宇宙空间有一艘宇宙飞船在做匀加速直线运动，一束光垂直于运动方向射入这艘飞船.船外静止的观察者当然会看到这束光是沿直线传播的，但是飞船中的观察者以飞船为参考系看到的却是另外一番情景.为了记录光束在飞船中的径迹，他在船中等距离地放置一些半透明的屏(如图)，光可以透过这些屏，同时在屏上留下光点.由于飞船在前进，光到达下一屏的位置总会比到达上一展的位置更加靠近船尾.如果飞船做匀速直线运动，光在任何相邻两屏之间飞行时，飞船前进的距离都相等，飞船上的观察者看到光的径迹仍是一条直线(如图中的虚线)，尽管直线的方向与船外静止观察者看到的直线方向不一样.如果飞船做匀加速直线运动，在光向右传播的同时，飞船的速度也在不断增大，因此船上观察者记录下的光的径迹是一条抛物线(如图中的实线).

　　根据等效原理，飞船中的观察者也完全可以认为飞船没有加速运动，而是在船尾方向存在一块巨大的物体，它的引力场影响了飞船内的物理过程.因此我们得出结论：物体的引力能使光线弯曲.

　　通常物体的引力场都太弱，20世纪初只能观测到太阳引力场引起的光线弯曲.由于太阳引力场的作用，我们有可能看到太阳后面的恒星(如图).但是，平时的明亮天空使我们无法观星，所以最好的时机是发生日全食的时候.1919年5月29日恰好有一次日全食，两支英国考察队分赴几内亚湾和巴行观测，其结果完全证实了爱因斯坦的预言.这是广义相对论的最早的验证.

　　时间间隔与引力场有关 引力场的存在使得空间不同位置的时间进程出现差别.

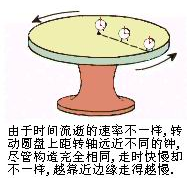
　　我们考察一个转动的巨大圆盘(如图).从地面上看，圆盘上除转动轴的位置外，各点都在做加速运动，越是靠近边缘，加速度越大，方向指向盘心.从地面上还会看到，越是靠近边缘的点，速度越大.根据狭义相对论，同一个过程，越是发生在靠近边缘的位置，这个过程所持续的时间就越长.或者说，靠近边缘位置的时间进程比较缓慢.

　　再以圆盘本身为参考系研究这个现象.圆盘上的人认为，盘上存在着一个引力场，方向由盘心指向边缘.既然靠近边缘位置的时间进程比较缓慢，盘上的人就可以得出结论：在引力势较低的位置，时间进程比较慢.

　　宇宙中有一类恒星，体积很小，质量却不小，叫做矮星.矮星表面的引力很强，引力势比地球表面低得多.矮星表面的时间进程比较慢，那里的原子发光的频率比同种原子在地球上发光的频率低，看起来偏红.这个现象叫做引力红移，已经在天文观测中得到证实.现代技术也能够在地球上验证引力红移.

　　杆的长度与引力场有关 仍然考察转动的圆盘.同样的杆，放在盘上的不同位置，它们随盘运动的速度就不一样，根据狭义相对论，它们的长度也就不一样，越是靠近边缘，杆就越短.盘上的人也观察到了这种差别，不过他以圆盘为参考系，认为盘是静止的，同时他还认为盘上各点存在着指向圆盘边缘的引力，因此他得出结论：引力势越低的位置，杆的长度越短.

　　杆的长度和引力场的分布有关，这个现象反映出这样的事实，即由于物质的存在，实际空间并不是均匀的，这和我们过去的观念有很大的差别.打个比方，一块布上面的格子是整齐的(如图甲)，如果用手向下压，格子就弯曲了(如图乙).物理学借用了“弯曲”这个词，通常说，由于物质的存在，实际的空间是弯曲的.

　　行星沿椭圆轨道绕太阳运动，有时离太阳近些，有时远些.太阳的巨大质量使它周围的空间发生弯曲，其结果是，行星每公转一周它的轨道的长轴都比上一个周期偏转一个角度，这个现象叫做行星轨道的进动.理论分析表明只有水星轨道的进动比较显著，达到约每世纪0.01°.这个现象早在广义相对论出现之前就已经发现，只是无法解释，所以它实际是广义相对论的最早的佐证.

　　广义相对论与几何学最后，我们再次回到转动的圆盘.狭义相对论告诉我们，只有沿着运动方向的长度发生变化，垂直于运动方向的长度不会变化;如果以圆盘为参考系，就可以说，沿着引力方向的空间尺度没有变化，只有垂直于引力方向的空间尺度发生了改变.这一点具有非常深刻的意义，因为这时测量圆盘的周长和直径，它们的比值就不再是3.141 59…，而是别的值，三角形的内角和也不会是180°了……简而言之，由于实际空间是弯曲的，我们学习的几何学已经不适用了.

　　几何学反映的是人对空间关系的认识.有史以来人们只是在比较小的空间尺度中接触到比较弱的引力场.这种情况下空间的弯曲可以忽略，在此基础上人类发展了欧几里得几何学，它反映了平直空间的实际.广义相对论告诉我们实际空间是弯曲的，因此描述实际空间的应该是更具有一般意义的非欧几何.不过，作为非欧几何的特例，欧几里得几何学在它的适用范围内仍是正确的，还将继续发挥作用.

　　1905年爱因斯坦发表狭义相对论后，他开始着眼于如何将引力纳入狭义相对论框架的思考。以一个处在自由落体状态的观察者的理想实验为出发点，他从1907年开始了长达八年的对引力的相对性理论的探索。在历经多次弯路和错误之后，他于1915年11月在普鲁士科学院上作了发言，其内容正是著名的爱因斯坦引力场方程。这个方程描述了处于时空中的物质是如何影响其周围的时空几何，并成为了爱因斯坦的广义相对论的核心。

　　爱因斯坦的引力场方程是一个二阶非线性偏微分方程组，数学上想要求得方程的解是一件非常困难的事。爱因斯坦运用了很多近似方法，从引力场方程得出了很多最初的预言。不过很快天才的天体物理学家卡尔·史瓦西就在1916年得到了引力场方程的第一个非平庸精确解——史瓦西度规，这个解是研究星体引力坍缩的最终阶段，即黑洞的理论基础。在同一年，将史瓦西几何扩展到带有电荷的质量的研究工作也开始进行，其最终结果就是雷斯勒-诺斯特朗姆度规，其对应的是带电荷的静态黑洞。1917年爱因斯坦将广义相对论理论应用于整个宇宙，开创了相对论宇宙学的研究领域。考虑到同时期的宇宙学研究中静态宇宙的学说仍被广为接受，爱因斯坦在他的引力场方程中添加了一个新的常数，这被称作宇宙常数项，以求得和当时的“观测”相符合。然而到了1929年，哈勃等人的观测表明我们的宇宙处在膨胀状态，而相应的膨胀宇宙解早在1922年就已经由亚历山大·弗里德曼从他的弗里德曼方程(同样由爱因斯坦场方程推出)得到，这个膨胀宇宙解不需要任何附加的宇宙常数项。比利时牧师勒梅特应用这些解构造了宇宙大爆炸的最早模型，模型预言宇宙是从一个高温高致密状态演化来的。爱因斯坦其后承认添加宇宙常数项是他一生中犯下的最大错误。

　　在那个时代，广义相对论与其他物理理论相比仍保持了一种神秘感。由于它和狭义相对论相融洽，并能够解释很多牛顿引力无法解释的现象，显然它要优于牛顿理论。爱因斯坦本人在1915年证明了广义相对论是如何解释水星轨道的反常近日点进动的现象，其过程不需要任何附加参数(所谓“敷衍因子”)。另一个著名的实验验证是由亚瑟·爱丁顿爵士率领的探险队在非洲的普林西比岛观测到的日食时的光线在太阳引力场中的偏折，其偏折角度和广义相对论的预言完全相符(是牛顿理论预言的偏折角的两倍)，这一发现随后被全球报纸竞相报导，一时间使爱因斯坦的理论名声赫赫。但是直到1960年至1975年间，广义相对论才真正进入了理论物理和天体物理主流研究的视野，这一时期被称作广义相对论的黄金时代。物理学家逐渐理解了黑洞的概念，并能够通过天体物理学的性质从类星体中识别黑洞。在太阳系内能够进行的更精确的广义相对论的实验验证进一步展示了广义相对论非凡的预言能力，而相对论宇宙学的预言也同样经受住了实验观测的检验。