



绝对太有才的创意
绝对太有才的创意,某广告公司从事文案策划的张山最近有些苦恼,因为女友琳琳对他不冷不热的,虽然他是热
某广告公司从事文案策划的张山最近有些苦恼,因为女友琳琳对他不冷不热的,虽然他是热情万丈,但总担心求婚不能遂愿,不敢贸然行动。
经过一个星期的紧张策划,一个大胆的策划方案在张山的苦思冥想中成竹在胸。张山特意不惜血本在世纪大酒店10楼的旋转餐厅预订一个午餐,约会女友琳琳共进午餐。两个人开开心心地边聊边吃,情意绵绵。大约30分钟之后,服务员送来一束玫瑰花,张山接过来玫瑰花,看到对面楼上4米×6米的巨幅广告悬挂妥当之后,跪在女友的面前,真心地说:“琳琳,嫁给我,好吗?”琳琳刹那间发愣之后,笑着说:“我还没有想好是否决定嫁给你……”她不由得把目光转向窗外,突然发现对面楼上悬挂着一幅巨型广告条幅:上面有她和张山的照片,两张照片中用鲜红大字写着:“琳琳,我真心爱你,嫁给我!”琳琳坐在座位上能够清清楚楚地看到巨幅条幅上的照片和文字。琳琳的心里顿时柔情似水,感动得一塌糊涂,幸福的眼泪顺着脸颊恣意流淌,滴落在玫瑰花上。琳琳哭着说:“张山,亲爱的,我嫁给你!”
张山的求婚策划方案取得了圆满的成功,心里暗想,“没有想到,真的可以这样表达爱情,比我想到的美好结果还要美好!”
第二天,张山收到琳琳发来的短信:“张山,经过深思熟虑之后,我认定我们结婚肯定不会幸福,还是做朋友吧。”
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。
——— 没有了 ———
编辑:阿族小谱

文章价值打分
- 有价值
- 一般般
- 没价值
当前文章打 0 分,共有 0 人打分
文章观点支持

0

0
文章很值,打赏犒劳一下作者~

发表评论
写好了,提交
{{item.label}}
{{commentTotal}}条评论
{{item.userName}}
发布时间:{{item.time}}
{{item.content}}
回复
举报


打赏作者
“感谢您的打赏,我会更努力的创作”
— 请选择您要打赏的金额 —
{{item.label}}


{{item.label}}

打赏成功!
“感谢您的打赏,我会更努力的创作”
返回
打赏
私信
推荐阅读
· 创意写作
概括创意写作,技术上可以被理解为任何没有剽窃成分的原创写作。在这个情况下,写作是被传统的称作文学的一个更当代,更过程主导的名称,而且涵盖各种文艺作品之类型。专业写作的行为,也不被排除在创意写作之外――两者可以同时进行。MARYLEEMARKSBERRY的《创作的基础》中引用了PAULWITTY以及LOULABRANT的《教育人类语言》对创意写作的定义,其记录了:学术界的创意写作与相当于教育学生架构文章于语言规则的写作班不同的是,创意写作是集中于学生的自我表达。当创意写作作为教育题材的时候一般都是在舞台上。如果不贯彻12年教育,也许最精炼的创意写作教育就只会集中发生在大学里面了。在大部分战后重开的大学里面,创意写作的重视程度变得日益明显。在正规创意写作刚开始的时候,教育方案创意写作方案,基本上适用于高中等级的作者乃至大学毕业生。这些方案传统上与学院的英语部联接,但这个简介近来不断受到质疑,以...
· 宋代状元留下的绝对,你对得出吗?央视报道28代孙的生活太让人羡慕!

提到文坛兴盛的朝代,那宋代绝对是首屈一指了。而宋朝也孕育出江浙一带不少的文坛轶事。今天阿族要分享的,就是浙江一位王姓状元留下的文坛轶事。王十朋其人王十朋(1112年-1171年),字龟龄,号梅溪,温州乐清(浙江乐清)人,南宋作家。北宋徽宗政和二年(公元1112年)十月二十八日生于乐清左原(今浙江省乐清市梅溪村)。俗话说出名趁早,王十朋就是如此。王他少时颖悟强记,七岁入塾,十四岁先后在鹿岩乡塾、金溪邑馆、乐清县学读书,学通经史,诗文名闻远近。十九岁时写出“北斗城池增王气,东瓯山水发清辉”的名句。其才华震动了浙南的诗坛。因为秦侩等奸臣当道,政治腐败,直到四十六岁,被宋高宗亲自擢选为状元。江心屿千古名对据说年轻时,王十朋常在浙江温州的江心寺蹭吃蹭喝,借宿读书。方丈并不生气,只请他为寺庙题下了一副对联。——“云朝朝朝朝朝朝朝朝散;潮长长长长长长长长消。”从内容上来说,上联写天上的白云,下联写江边的...
· 创意故事
创新点:该项目使用专用集成电路,液晶眼镜片的非线性光电特性进行统和,实现液晶眼镜片各向异性、不确定的光传导能力自适应控制,以适应人眼需要。变色既快又稳。应用:眼镜
· 创意故事
北京京港恒星科技发展有限公司发明的科技创新产品“抑菌防辐射面料”,其主要构成是牛奶蛋白银纤维。牛奶蛋白纤维的特点:柔软、保暖、耐磨、透气、导湿等,PH值6.8,呈微酸性,不利于细菌生长,有抑菌功能。银纤维材料是使用纳米植入技术,以化学纤维、面纤维为基础,使银离子与纤维素牢固结合在一起,稳定性好。其特点:屏蔽辐射、天然杀菌。
· 绝对值
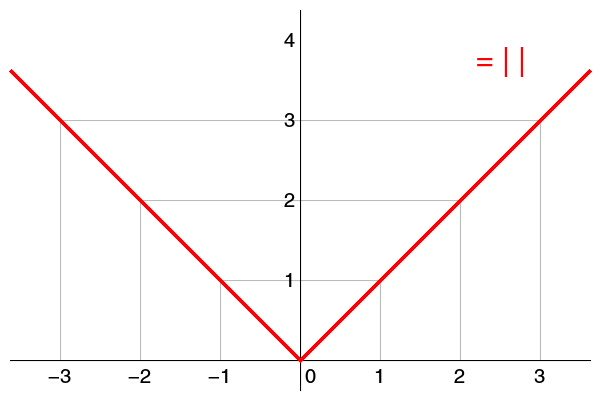
实数的绝对值实数绝对值的平面座标图若实数a≠≠-->0{\displaystylea\neq0},则在两对称互对称的数a{\displaystylea}和−−-->a{\displaystyle-a}中必有且仅有一个数大于0,这个大于0的数就称为数a{\displaystylea}和数−−-->a{\displaystyle-a}的绝对值,记为|a|=|−−-->a|{\displaystyle\left|a\right|=\left|-a\right|},0的绝对值为0。一个数的绝对值永远非负,没有负号,某数的绝对值表示为|{\displaystyle|}某数|{\displayst实数e|}。对于所有实数x{\displaystylex}:若x{\displ负数stylex}是负数,|x|=−−-->x{\displaystyle|x|=-x}(即是−−-...
关于我们

关注族谱网 微信公众号,每日及时查看相关推荐,订阅互动等。
APP下载

下载族谱APP 微信公众号,每日及时查看

扫一扫添加客服微信

















